Why not everyone who smokes develop cancer or who eats a lot develop fatty liver disease? Predicting diseases with machine learning

Last updated on Oct 1, 2019 24 min read

We are much better at handling diseases than 30 years ago. For example cancer survival rates are much higher now. The significant portion of this increase can be attributed directly to our ability to detect and diagnose cancer earlier. Also, use of insulin and other drugs to control blood glucose in diabetic patients reduced the risk of developing coronary diseases.

We are at constant hunt for finding new evidence which environmental factors put us at risk for which diseases. Exposure to certain chemicals (smoking, industry workers) can cause certain types of cancer and our eating habits might put us at higher risk for developing diseases such us diabetes or liver fibrosis.

Figure 1: Photo by Heather Ford on Unsplash

But not everyone who smokes develop lung cancer or who eats a lot of sugar develop fatty liver disease. Our genetic background makes us prone or immune to develop different diseases. This is where data science might enable us with new insights connecting the risk factors to our genetic make up. And the better we are at identifying high risk patients the better treatment for the patients.

We are developing new technologies at lightning speed. We can now analyse genes from a single cell which was not even possible couple of years back, and extract the knowledge hidden in rare genes or rare cell types.

Sensors collect real time data from patients e.g. in diabetic patients, we started to pool data (real world evidence) generated during the actual use of drugs by patients (e.g. OMOP common data model. The data that we have access now is enormous and is growing rapidly.

Data Science tools are more than ever needed to mold this data into better therapies.

We can build new machine learning models and;

diagnose diseases earlier
develop better drugs which are more effective and have less side effects
identify patient groups which benefit most from existing drugs

We will be able to understand why certain diseases develop and their connections to our lifestyle by using multiple types of data we accumulate.

Let’s look at an example and see how we can do this.

First part in any data science process is problem formulation.

Problem formulation

Our problem, or question that we want to answer is:

Can we predict which patients will develop Diabetes by building a Machine learning algorithm?

We will predict a Binary Outcome: Diabetes vs Healthy by using 8 medical indicators.

Overview of the data

The Pima Indians of Arizona and Mexico have contributed to numerous scientific gains. Their involvement has led to significant findings on genetics of both type 2 diabetes and obesity.

The medical indicators recorded are;

Pregnancies: Number of times pregnant
Glucose: Plasma glucose concentration a 2 hours in an oral glucose tolerance test
BloodPressure: Diastolic blood pressure (mm Hg)
SkinThickness: Triceps skin fold thickness (mm)
Insulin: 2-Hour serum insulin (mu U/ml)
BMI: Body mass index (weight in kg/(height in m)^2)
DiabetesPedigreeFunction: Diabetes pedigree function
Age: Age (years)
Outcome: Class variable (0 or 1)

Data acquisition

You can download the Pima Indians Diabetes Dataset from Kaggle and load it in RStudio.

Setting up and loading in the data.

diabetes <- read.csv("posts_data/diabetes.csv")
library(tidyverse) # Includes packages: ggplot2, dplyr, tidyr, readr, 
                   # purrr, tibble, stringr, forcats
library(reshape2) # Main function: melt()
library(ggcorrplot)
library(pROC)
library(lattice)
library(caret)
library(waffle)
library(compareGroups) # Main functions: compareGroups(), createTable()

Next step in our data science process is to check whether the data quality is good.

Data Quality control

Before running any algorithm a good starting point is to check obvious mistakes and abnormalities in your data.

I would first look at Missing values, NAs, variable ranges (min, max values). A very extreme value might be basically a typing error.

Understand your Data

How big is the data? Classes of variables?

dim(diabetes)

## [1] 768   9

knitr::kable(sapply(diabetes, class))

	x
Pregnancies	integer
Glucose	integer
BloodPressure	integer
SkinThickness	integer
Insulin	integer
BMI	numeric
DiabetesPedigreeFunction	numeric
Age	integer
Outcome	integer

I look which atomic data types my variables are. I see that the outcome variable is represented as an integer. We will keep this in mind because many machine learning models will accept the binary outcome when converted to a factor atomic data type.

Next, what catches my attention is unexpected zeros in Insulin. See below.

knitr::kable(head(diabetes))

Pregnancies	Glucose	BloodPressure	SkinThickness	Insulin	BMI	DiabetesPedigreeFunction	Age	Outcome
6	148	72	35	0	33.6	0.627	50	1
1	85	66	29	0	26.6	0.351	31	0
8	183	64	0	0	23.3	0.672	32	1
1	89	66	23	94	28.1	0.167	21	0
0	137	40	35	168	43.1	2.288	33	1
5	116	74	0	0	25.6	0.201	30	0

Missing Values

Summary gives a good overview of the variables. Any missing data would show up here listed as “NA’s”. But we have none here.

summary(diabetes)

##   Pregnancies        Glucose      BloodPressure    SkinThickness  
##  Min.   : 0.000   Min.   :  0.0   Min.   :  0.00   Min.   : 0.00  
##  1st Qu.: 1.000   1st Qu.: 99.0   1st Qu.: 62.00   1st Qu.: 0.00  
##  Median : 3.000   Median :117.0   Median : 72.00   Median :23.00  
##  Mean   : 3.845   Mean   :120.9   Mean   : 69.11   Mean   :20.54  
##  3rd Qu.: 6.000   3rd Qu.:140.2   3rd Qu.: 80.00   3rd Qu.:32.00  
##  Max.   :17.000   Max.   :199.0   Max.   :122.00   Max.   :99.00  
##     Insulin           BMI        DiabetesPedigreeFunction      Age       
##  Min.   :  0.0   Min.   : 0.00   Min.   :0.0780           Min.   :21.00  
##  1st Qu.:  0.0   1st Qu.:27.30   1st Qu.:0.2437           1st Qu.:24.00  
##  Median : 30.5   Median :32.00   Median :0.3725           Median :29.00  
##  Mean   : 79.8   Mean   :31.99   Mean   :0.4719           Mean   :33.24  
##  3rd Qu.:127.2   3rd Qu.:36.60   3rd Qu.:0.6262           3rd Qu.:41.00  
##  Max.   :846.0   Max.   :67.10   Max.   :2.4200           Max.   :81.00  
##     Outcome     
##  Min.   :0.000  
##  1st Qu.:0.000  
##  Median :0.000  
##  Mean   :0.349  
##  3rd Qu.:1.000  
##  Max.   :1.000

Plotting how the variables are distributed will give a good overview to spot problems.

I will change the data format so that I can plot all the variables in different facets. melt() function from reshape2 package can create a tall version of my data.

This function will collect all variable names in one column and corresponding values in the next column. This data structure will allow me to plot all variables together.

gg <- melt(diabetes)

# Check how the new data structure looks like
head(gg)

##      variable value
## 1 Pregnancies     6
## 2 Pregnancies     1
## 3 Pregnancies     8
## 4 Pregnancies     1
## 5 Pregnancies     0
## 6 Pregnancies     5

# Plot all variables
ggplot(gg, aes(x=value, fill=variable)) +
  geom_histogram(binwidth=5) + 
  theme(legend.position = "none") +
  facet_wrap(~variable)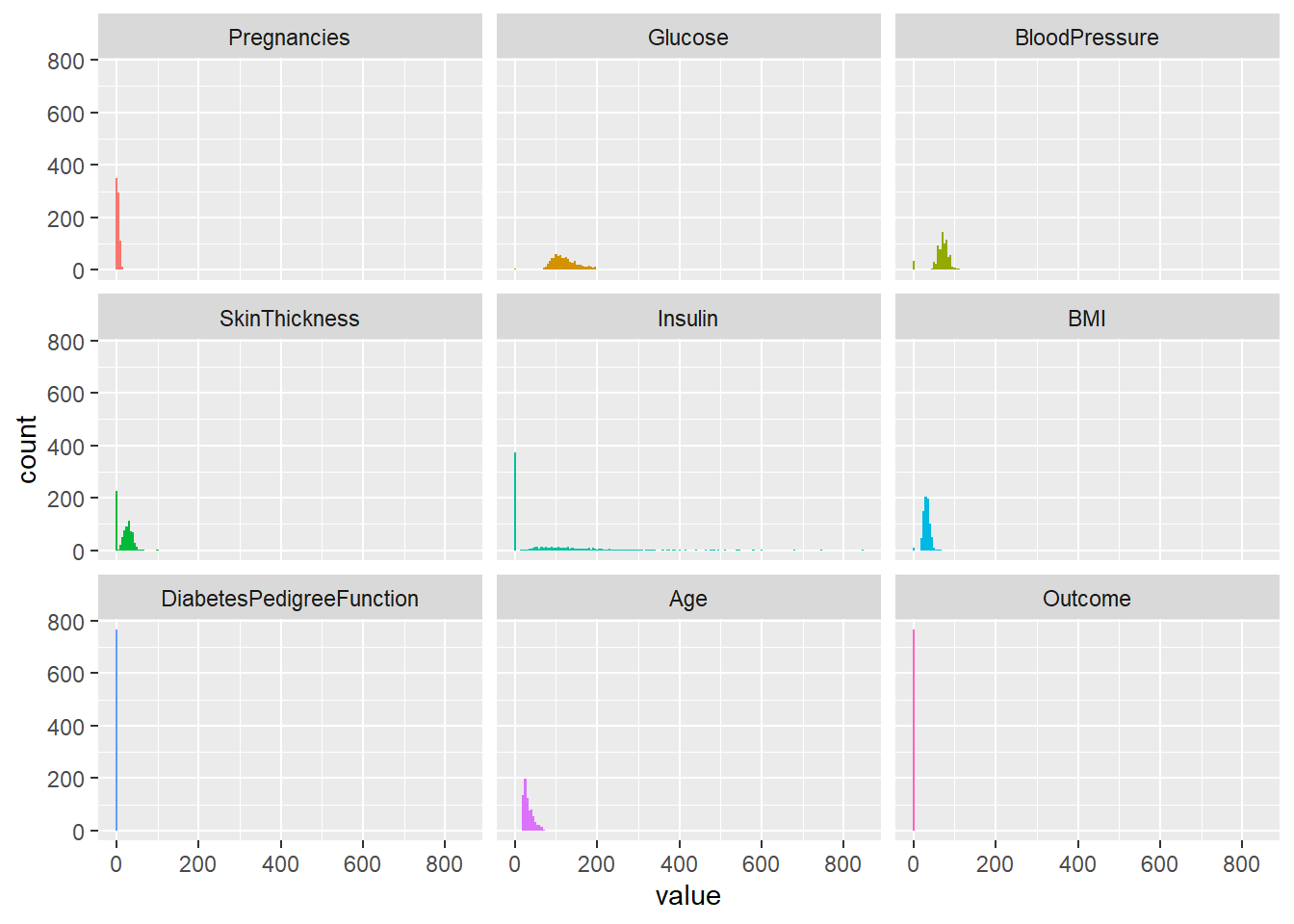

Multiple variables have peaks at zero. E.g. Skin Thickness and Insulin. It is not possible that those variables are zero.

I want to know how many zeros each variables has. In cases where the numbers are small we might remove them. Let’s figure it out with a for loop. and then visualize on a waffle plot.

I am selecting only variables from 2 to 6 because only those can’t be zero. Let’s count number of zeros.

How to count zeros in each column?

Approach 1: Using a for loop, which() function and []

zero_rows <- list()
for(i in 2:6){
zero_rows[[i]] <- length(which(diabetes[,i] == 0))  
}
rows_with_zero <- unlist(zero_rows)
rows_with_zero

## [1]   5  35 227 374  11

As a bonus, I recommend using dplyr package.

Approach 2: Much simpler with dplyr summarise_all() function

zeros <- diabetes[,2:6] %>%  summarise_all(funs(sum(.==0)))
t(zeros)

##               [,1]
## Glucose          5
## BloodPressure   35
## SkinThickness  227
## Insulin        374
## BMI             11

Feed those numbers into a waffle plot.

zeros <- c("Glucose" =zeros[1,1], "Blood Pressure" = zeros[1,2], 
           "Skin Thickness"= zeros[1,3], "Insulin" =zeros[1,4], 
           "BMI" = zeros[1,5])
waffle(zeros, rows=20) + 
  theme(text = element_text(size=15)) + 
  ggtitle("Number of rows with zero")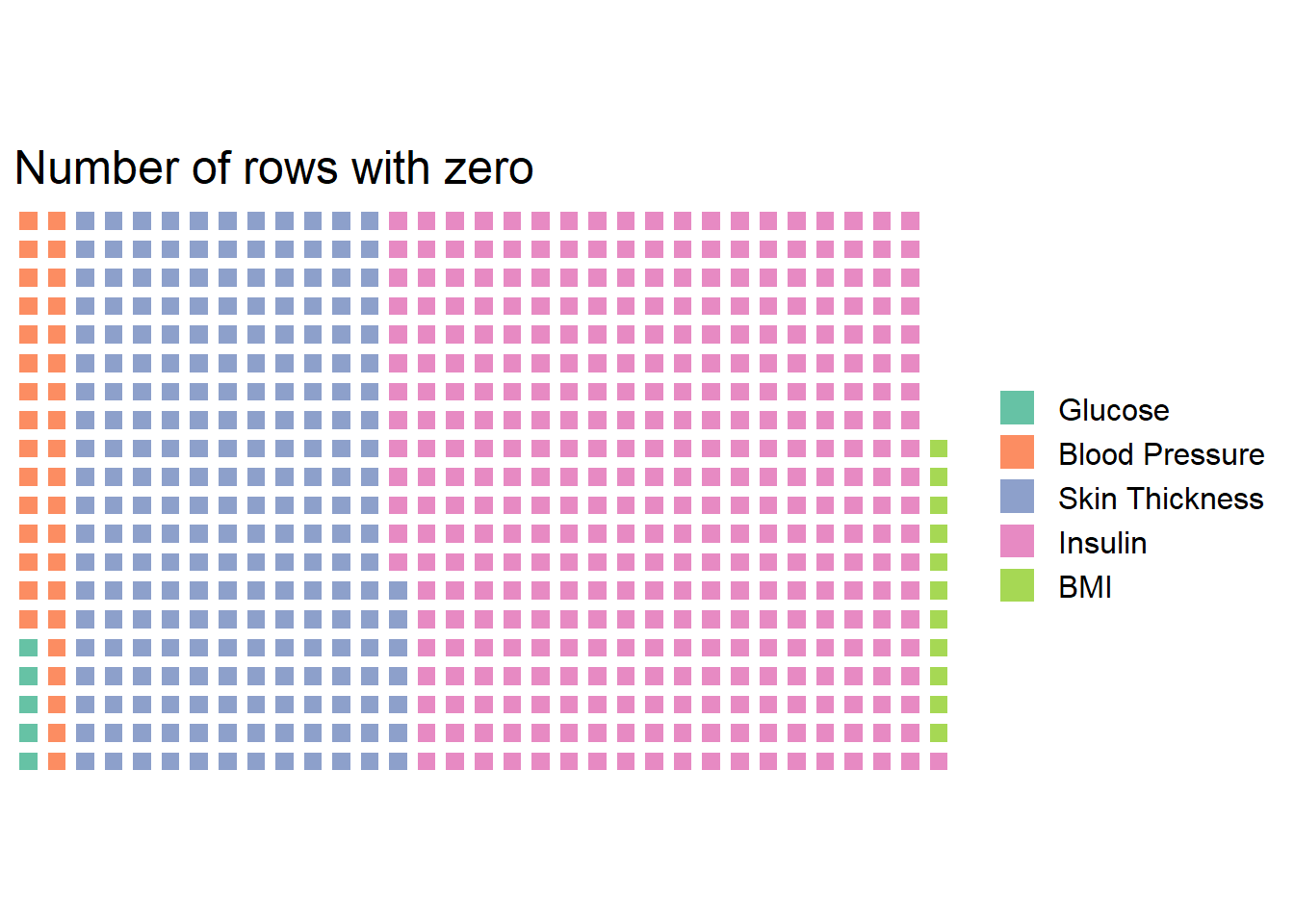

For instance, 374 rows of Insulin are zero. Other variables also contain zeros. Something is wrong. It is impossible to have Blood Pressure or Glucose levels at 0. It is unlikely that those are simply entry mistakes. It seems missing values are filled with zeros in the data collection phase.

How to circumvent this?

Convert all zeroes to NAs and then perform Median Imputation

Most models require numbers, and can’t handle missing data. Throwing out rows is not a good idea since it can lead to biases in your dataset and generate overconfident models.

Median imputation lets you model data with missing values. By replacing them with their medians.

To do this, I need to change zeros to missing values. I will do this for all the predictors which zero is not plausible(columns 2 to 6).

for(i in 2:6){
# Convert zeros to NAs
diabetes[, i][diabetes[, i] == 0] <- NA
# Calculate median
median <- median(diabetes[, i], na.rm = TRUE)
diabetes[, i][is.na(diabetes[, i])] <- median
}

Check if it really happened.

knitr::kable(head(diabetes))

Pregnancies	Glucose	BloodPressure	SkinThickness	Insulin	BMI	DiabetesPedigreeFunction	Age	Outcome
6	148	72	35	125	33.6	0.627	50	1
1	85	66	29	125	26.6	0.351	31	0
8	183	64	29	125	23.3	0.672	32	1
1	89	66	23	94	28.1	0.167	21	0
0	137	40	35	168	43.1	2.288	33	1
5	116	74	29	125	25.6	0.201	30	0

For instance, I see that zero values in the insulin variable is replaced with median of insulin which is 125.

I will also look at the differences between variables in diabetic versus healthy groups so that I know more which variables might play a role in the Outcome.

I can also use dplyr functions but I will use compareGroups package because it creates a nice output of the summary statistics in a table format. compareGroups() function will do the analysis and createTable() will output it in a nice format.

base <- compareGroups(Outcome~Pregnancies+Glucose+BloodPressure+
                        SkinThickness+Insulin+BMI +
                        DiabetesPedigreeFunction+Age, 
                        data = diabetes)

summary_stats <- createTable(base, show.ratio = FALSE, show.p.overall=TRUE)
summary_stats

## 
## --------Summary descriptives table by 'Outcome'---------
## 
## __________________________________________________________ 
##                               0           1      p.overall 
##                             N=500       N=268              
## ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ 
## Pregnancies              3.30 (3.02) 4.87 (3.74)  <0.001   
## Glucose                  111 (24.7)  142 (29.6)   <0.001   
## BloodPressure            70.9 (11.9) 75.1 (12.0)  <0.001   
## SkinThickness            27.7 (8.55) 31.7 (8.66)  <0.001   
## Insulin                  128 (74.4)   165 (101)   <0.001   
## BMI                      30.9 (6.50) 35.4 (6.60)  <0.001   
## DiabetesPedigreeFunction 0.43 (0.30) 0.55 (0.37)  <0.001   
## Age                      31.2 (11.7) 37.1 (11.0)  <0.001   
## ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

You can see here that couple of variables are significantly higher in diabetic patients, such as Pregnancies, glucose, insulin, bmi and so on. This can give hints on what to expect from the linear model.

So far, we made some visualizations to understand the dataset better, made some quality checks and cleaning.

Now, the data is ready for the modeling phase.

Modeling the data (build, fit and validate a model)

Before going into any complicated model starting with a simple model is a good idea. It might do surprisingly well and will give us more insights.

Model assumptions

One of the assumptions of logistic regression that it requires large sample size.

What should be the minimum sample size for running logistic regression?

Minimum sample size is given by the following formula:

N = 10 k / p

where,

p is the proportion of the least frequent class of the Outcome variable. We have 768 cases of which 500 are diabetic and 268 non diabetic.

p = 268/768 = 0.34

And k is the number of covariates ( the number of predictor variables)

k = 8

N = 10 * 8 / 268/768 N = 229

Since we have a total of 768 cases we can apply logistic regression model.

Logistic Regression Model

We will create two random subsets of our data in 80/20 proportion as training and test data. Training data will be used to build our model and test data will be reserved to validate it.

set.seed(22)
# Create train test split
sample_rows <- sample(nrow(diabetes), nrow(diabetes) * 0.8)
# Create the training dataset
dia_train <- diabetes[sample_rows, ]
# Create the test dataset
dia_test <- diabetes[-sample_rows, ]

# Build a logistic regression model with the train data
glm_dia <- glm(Outcome ~ .,data = dia_train, family = "binomial")
summary(glm_dia)

## 
## Call:
## glm(formula = Outcome ~ ., family = "binomial", data = dia_train)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -2.5941  -0.7143  -0.3887   0.7330   2.1417  
## 
## Coefficients:
##                           Estimate Std. Error z value Pr(>|z|)    
## (Intercept)              -9.371525   0.926425 -10.116  < 2e-16 ***
## Pregnancies               0.108782   0.036022   3.020 0.002529 ** 
## Glucose                   0.036465   0.004309   8.462  < 2e-16 ***
## BloodPressure            -0.010359   0.009470  -1.094 0.273974    
## SkinThickness             0.005730   0.014928   0.384 0.701105    
## Insulin                  -0.002056   0.001279  -1.607 0.107995    
## BMI                       0.102303   0.021009   4.870 1.12e-06 ***
## DiabetesPedigreeFunction  1.154731   0.327099   3.530 0.000415 ***
## Age                       0.021617   0.010619   2.036 0.041780 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 793.94  on 613  degrees of freedom
## Residual deviance: 570.22  on 605  degrees of freedom
## AIC: 588.22
## 
## Number of Fisher Scoring iterations: 5

The summary shows us not all the variables play a role in predicting outcome. The significant correlations was found for Pregnancies, Glucose, BMI and Pedigree function.

The predict function will give us probabilities. To compute our model accuracy we need to convert them to class predictions by setting a threshold level.

# We will predict the Outcome for the test data
p<-predict(glm_dia, dia_test)
# Choose a threshold 0.5 to calculate the accuracy of our model
p_05 <- ifelse(p > 0.5, 1, 0)
table(p_05, dia_test$Outcome)

##     
## p_05  0  1
##    0 88 23
##    1 12 31

We will build a confusion matrix to calculate how accurate our model is in this particular random train/test split and at 0.5 threshold level.

conf_mat <- table(p_05, dia_test$Outcome)
accuracy <- sum(diag(conf_mat))/sum(conf_mat)
accuracy

## [1] 0.7727273

roc function pROC package, can plot us a ROC curve which tests accuracy of our model at multiple threshold levels and is a good estimate on how well our model is performing.

# Calculate AUC(Area under the curve)
roc(dia_test$Outcome, p)

## Setting levels: control = 0, case = 1

## Setting direction: controls < cases

## 
## Call:
## roc.default(response = dia_test$Outcome, predictor = p)
## 
## Data: p in 100 controls (dia_test$Outcome 0) < 54 cases (dia_test$Outcome 1).
## Area under the curve: 0.8446

However, this process is little fragile, presence or absence of a single outlier might vastly change the results you might get from a given random train/test split.

A better approach than a simple train/test split is using multiple test sets and averaging their accuracies.

Let’s test that. I will create 1, 30 or 1000 random test sets, build models and compare their accuracies.

How to apply multiple train/test split

To do this, I will write a function where I can choose number of independent train/test splits.

It will return me an average value of the accuracy(auc) of the model after chosen number of iteration. The higher the number of random splits the more stable your estimated AUC will be.

Let’s see how it will work out for our diabetes patients.

# I will define my function as follows
multi_split <- function(x){
sample_rows <- list()
dia_train <- list()
dia_test <- list()
glm <- list()
p <-  list()
roc_auc <- list()
for(i in 1:x){
  sample_rows[[i]] <- sample(nrow(diabetes), nrow(diabetes) * 0.8)
  # Create the training dataset
  dia_train[[i]] <- diabetes[sample_rows[[i]], ]
  # Create the test dataset
  dia_test[[i]] <- diabetes[-sample_rows[[i]], ]
  glm[[i]] <- glm(Outcome ~ .,data = dia_train[[i]], family = "binomial")
  p[[i]] <- predict(glm[[i]], dia_test[[i]])
  
  # Calculate AUC for all "x" number of random splits
  roc_auc[[i]] <- roc(dia_test[[i]]$Outcome, p[[i]])$auc[1]
  glm_mean <- mean(unlist(roc_auc))
}
print(mean(unlist(roc_auc)))
}

Let’s calculate the average AUC of our model after different number of random splits.

I will run my multi_split() function 3x for 1, 30 and 1000 random train/test splits. I can then compare variances at each level of sampling.

Here are the results from my multi_site function at each randomization.

auc_1_1 <- multi_split(1)

## [1] 0.8737245

auc_1_2 <- multi_split(1)

## [1] 0.8271277

auc_1_3 <- multi_split(1)

## [1] 0.824344

auc_30_1 <- multi_split(30)

## [1] 0.8399321

auc_30_2 <- multi_split(30)

## [1] 0.8492238

auc_30_3 <- multi_split(30)

## [1] 0.8294277

auc_1000_1 <- multi_split(1000)

## [1] 0.8356283

auc_1000_2 <- multi_split(1000)

## [1] 0.836047

auc_1000_3 <- multi_split(1000)

## [1] 0.8345809

Let’s compare Variance levels at 1, 30 and 1000 random splits

var(c(auc_1_1, auc_1_2, auc_1_3))

## [1] 0.0007695739

var(c(auc_30_1, auc_30_2, auc_30_3))

## [1] 9.809343e-05

var(c(auc_1000_1, auc_1000_2, auc_1000_3))

## [1] 5.702925e-07

What we see here as we increase the number of iterations to 30 and 1000 the variability gradually stabilizes around a trustable AUC of 0.835.

Seeing is believing. Let’s plot it.

# Create a data.frame containing accuracies
random_1X <- c(auc_1_1, auc_1_2, auc_1_3)
random_30X <- c(auc_30_1, auc_30_2, auc_30_3)
random_1000X <- c(auc_1000_1, auc_1000_2, auc_1000_3)

df_r <- data.frame(random_1X, random_30X, random_1000X)
df_r

##   random_1X random_30X random_1000X
## 1 0.8737245  0.8399321    0.8356283
## 2 0.8271277  0.8492238    0.8360470
## 3 0.8243440  0.8294277    0.8345809

# Here, I will reformat my data for easy plotting by using gather() function from tidyr
# It takes multiple columns, and gathers them into key-value pairs: it makes “wide” data longer.
df_long <- gather(df_r, sampling, auc)
df_long

##       sampling       auc
## 1    random_1X 0.8737245
## 2    random_1X 0.8271277
## 3    random_1X 0.8243440
## 4   random_30X 0.8399321
## 5   random_30X 0.8492238
## 6   random_30X 0.8294277
## 7 random_1000X 0.8356283
## 8 random_1000X 0.8360470
## 9 random_1000X 0.8345809

df_long$sampling <- factor(df_long$sampling, levels = c("random_1X", "random_30X", "random_1000X"))

# 
model_variation <- ggplot(df_long, aes(y=auc, x=sampling, fill=sampling)) + geom_boxplot() + theme(text = element_text(size=15), axis.title.x=element_blank(), legend.position = "none") + ggtitle("Variation in model performance")
model_variation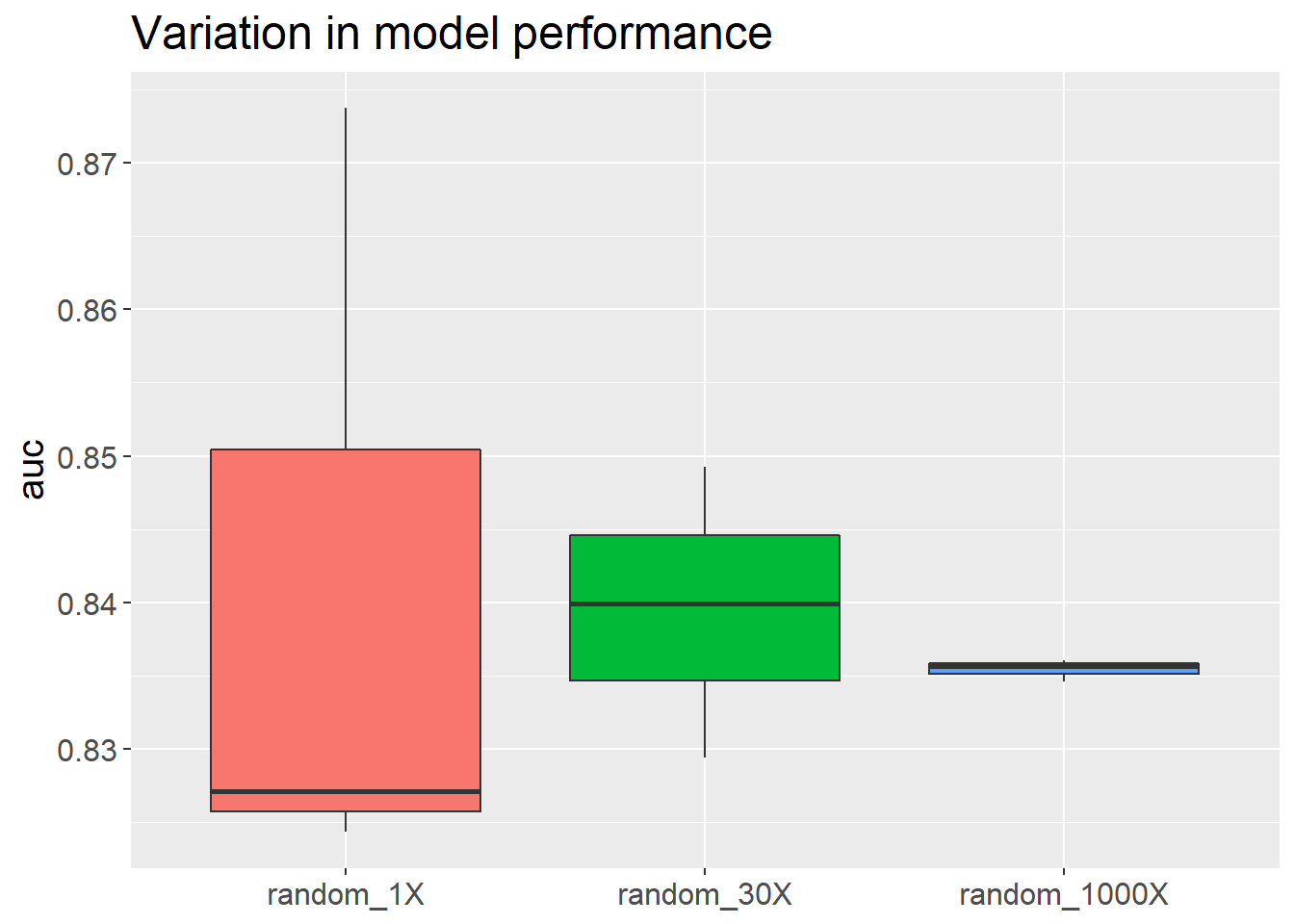

Great. We have an estimate of our model performance after 1000 random train/test splits. This process is also called Monte-Carlo Cross validation. This approach might give you a less variable, but more biased estimate.

A more common approach to estimate model performance is k-Fold cross Validation. Where the samples divided into k-folds and one fold is used as a test set, and the remaining k-1 as the training set. This process is run k times until all folds appear once in the test sample.

Logistic regression model with k-fold Cross Validation

I will switch here to caret package. With the Train() function we can test different types of machine learning algorithms and set the cross validation parameters.

To make the models below comparable I will create a custom cross validation fold object (d_folds) that I can apply to multiple models.

I will repeat the logistic regression model with 5 fold cross validation and then we can compare it to monte carlo cross validation.

# Convert Outcome to a factor with two levels
diabetes$Outcome <- ifelse(diabetes$Outcome == 1, "Yes", "No")
outcome <- diabetes$Outcome
d_folds <- createFolds(outcome, k=5)

# Create a dataframe without the outcome column
diab <- diabetes[,-9]

# MyControl
myControl <- trainControl(
    summaryFunction = twoClassSummary,
    classProbs = TRUE,
    verboseIter = TRUE,
    savePredictions = TRUE,
    index = d_folds
)
# Model_glm
model_glm <- train(x = diab, y = outcome,
                   metric = "ROC",
                   method = "glm",
                   family = binomial(),
                   trControl = myControl
)

## + Fold1: parameter=none 
## - Fold1: parameter=none 
## + Fold2: parameter=none 
## - Fold2: parameter=none 
## + Fold3: parameter=none 
## - Fold3: parameter=none 
## + Fold4: parameter=none 
## - Fold4: parameter=none 
## + Fold5: parameter=none 
## - Fold5: parameter=none 
## Aggregating results
## Fitting final model on full training set

model_glm

## Generalized Linear Model 
## 
## 768 samples
##   8 predictor
##   2 classes: 'No', 'Yes' 
## 
## No pre-processing
## Resampling: Bootstrapped (5 reps) 
## Summary of sample sizes: 154, 153, 153, 154, 154 
## Resampling results:
## 
##   ROC        Sens   Spec    
##   0.8136093  0.844  0.577431

Here, My model performance is 0.8136093

Glmnet model

# Model
model_glmnet <- train(x = diab, y = outcome,
                   metric = "ROC",
                   method = "glmnet", tuneGrid = expand.grid(
                          alpha = 0:1,
                          lambda = seq(0.0001, 1, length = 20)
                      ),
                   trControl = myControl
)

model_glmnet

## glmnet 
## 
## 768 samples
##   8 predictor
##   2 classes: 'No', 'Yes' 
## 
## No pre-processing
## Resampling: Bootstrapped (5 reps) 
## Summary of sample sizes: 154, 153, 153, 154, 154 
## Resampling results across tuning parameters:
## 
##   alpha  lambda      ROC        Sens    Spec       
##   0      0.00010000  0.8201210  0.8615  0.554096935
##   0      0.05272632  0.8227469  0.8725  0.541977831
##   0      0.10535263  0.8239613  0.8880  0.506537709
##   0      0.15797895  0.8242214  0.9005  0.482290806
##   0      0.21060526  0.8240544  0.9115  0.444025212
##   0      0.26323158  0.8238034  0.9210  0.420725929
##   0      0.31585789  0.8233937  0.9290  0.395548794
##   0      0.36848421  0.8230260  0.9365  0.357313627
##   0      0.42111053  0.8228119  0.9430  0.331201913
##   0      0.47373684  0.8224972  0.9505  0.306955010
##   0      0.52636316  0.8222639  0.9575  0.276166051
##   0      0.57898947  0.8220894  0.9615  0.254705499
##   0      0.63161579  0.8219008  0.9670  0.238852423
##   0      0.68424211  0.8217353  0.9690  0.217396218
##   0      0.73686842  0.8215489  0.9705  0.200604216
##   0      0.78949474  0.8214394  0.9725  0.178235166
##   0      0.84212105  0.8212995  0.9755  0.157704847
##   0      0.89474737  0.8210990  0.9785  0.138109107
##   0      0.94737368  0.8209896  0.9800  0.125976962
##   0      1.00000000  0.8208614  0.9805  0.111980004
##   1      0.00010000  0.8141708  0.8450  0.575553141
##   1      0.05272632  0.8232373  0.9040  0.505646599
##   1      0.10535263  0.8064789  0.9490  0.348028689
##   1      0.15797895  0.7982626  0.9865  0.118687242
##   1      0.21060526  0.7913587  0.9995  0.002803738
##   1      0.26323158  0.5552114  1.0000  0.000000000
##   1      0.31585789  0.5000000  1.0000  0.000000000
##   1      0.36848421  0.5000000  1.0000  0.000000000
##   1      0.42111053  0.5000000  1.0000  0.000000000
##   1      0.47373684  0.5000000  1.0000  0.000000000
##   1      0.52636316  0.5000000  1.0000  0.000000000
##   1      0.57898947  0.5000000  1.0000  0.000000000
##   1      0.63161579  0.5000000  1.0000  0.000000000
##   1      0.68424211  0.5000000  1.0000  0.000000000
##   1      0.73686842  0.5000000  1.0000  0.000000000
##   1      0.78949474  0.5000000  1.0000  0.000000000
##   1      0.84212105  0.5000000  1.0000  0.000000000
##   1      0.89474737  0.5000000  1.0000  0.000000000
##   1      0.94737368  0.5000000  1.0000  0.000000000
##   1      1.00000000  0.5000000  1.0000  0.000000000
## 
## ROC was used to select the optimal model using the largest value.
## The final values used for the model were alpha = 0 and lambda = 0.1579789.

plot(model_glmnet)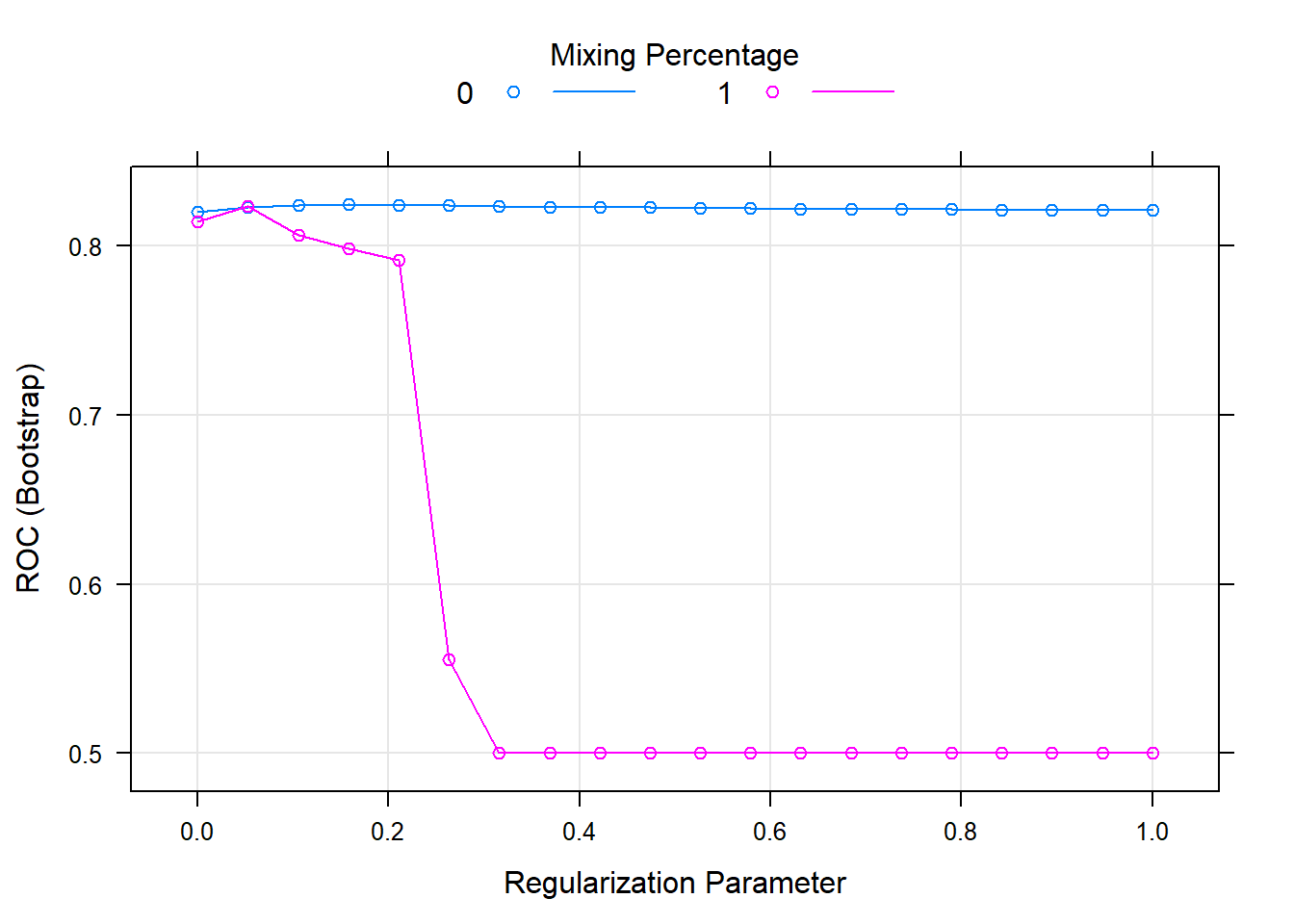

As we see in the plot, ridge regression (alpha = 0) performed better than the lasso at all lambda values.

Glmnet model performance is 0.8242214

Random forest model

One of the big diferences between random forest and linear models is that they require “tuning.”

Hyperparameters –> How the model is fit. Selected by hand.

advantages: no need to log transform or normalize, but they are less interpretable and slower than glmnet.

Random forests capture threshold effects and variable interactions. both of which occur often in real world data

mtry is the number of variables used at each split point in individual decision tree that make up the rf. Default is 3, I will use here 8.

tuneLength = how many different mtry values to be tested.

# Random forest model
model_rf <- train(x = diab, y = outcome,
                   tuneLength = 8,
                   metric = "ROC",
                   method = "ranger",
                   trControl = myControl
)

model_rf

## Random Forest 
## 
## 768 samples
##   8 predictor
##   2 classes: 'No', 'Yes' 
## 
## No pre-processing
## Resampling: Bootstrapped (5 reps) 
## Summary of sample sizes: 154, 153, 153, 154, 154 
## Resampling results across tuning parameters:
## 
##   mtry  splitrule   ROC        Sens    Spec     
##   2     gini        0.8155919  0.8565  0.5410389
##   2     extratrees  0.8247223  0.8730  0.5419474
##   3     gini        0.8142703  0.8490  0.5596827
##   3     extratrees  0.8241664  0.8650  0.5550185
##   4     gini        0.8098886  0.8440  0.5559617
##   4     extratrees  0.8244122  0.8595  0.5671376
##   5     gini        0.8096393  0.8475  0.5596914
##   5     extratrees  0.8244900  0.8550  0.5708498
##   6     gini        0.8075402  0.8460  0.5578309
##   6     extratrees  0.8231397  0.8530  0.5755401
##   7     gini        0.8063892  0.8415  0.5662117
##   7     extratrees  0.8213101  0.8515  0.5652728
##   8     gini        0.8058247  0.8335  0.5717931
##   8     extratrees  0.8209827  0.8485  0.5773788
## 
## Tuning parameter 'min.node.size' was held constant at a value of 1
## ROC was used to select the optimal model using the largest value.
## The final values used for the model were mtry = 2, splitrule =
##  extratrees and min.node.size = 1.

Random forest performance is 0.8247223

Gradient boost model

I will define manualy a grid to test hyperparameter values wider than set in default.

grid <- expand.grid(interaction.depth = c(1, 2, 3, 4, 5),
                 n.trees = (1:20)*50,  shrinkage = 0.01,
             n.minobsinnode = 10)
model_gbm <- train(x = diab, y = outcome,
                   metric = "ROC",
                   method = "gbm",
                   tuneGrid = grid,
                   trControl = myControl
)

model_gbm

## Stochastic Gradient Boosting 
## 
## 768 samples
##   8 predictor
##   2 classes: 'No', 'Yes' 
## 
## No pre-processing
## Resampling: Bootstrapped (5 reps) 
## Summary of sample sizes: 154, 153, 153, 154, 154 
## Resampling results across tuning parameters:
## 
##   interaction.depth  n.trees  ROC        Sens    Spec      
##   1                    50     0.7996312  0.9850  0.09252336
##   1                   100     0.8103617  0.9505  0.32756357
##   1                   150     0.8153748  0.9275  0.42350793
##   1                   200     0.8180549  0.9100  0.48598131
##   1                   250     0.8213254  0.8965  0.51863943
##   1                   300     0.8221740  0.8860  0.52983699
##   1                   350     0.8210830  0.8815  0.53729189
##   1                   400     0.8218884  0.8740  0.55409694
##   1                   450     0.8222721  0.8680  0.55874375
##   1                   500     0.8212831  0.8625  0.55593567
##   1                   550     0.8222189  0.8595  0.56525973
##   1                   600     0.8210507  0.8540  0.56620300
##   1                   650     0.8206810  0.8510  0.56806781
##   1                   700     0.8197731  0.8495  0.56806781
##   1                   750     0.8194073  0.8495  0.57180178
##   1                   800     0.8179990  0.8460  0.57459683
##   1                   850     0.8173591  0.8435  0.57459683
##   1                   900     0.8167653  0.8400  0.57272332
##   1                   950     0.8159870  0.8395  0.57366225
##   1                  1000     0.8155800  0.8375  0.57738752
##   2                    50     0.8097645  0.9705  0.19896110
##   2                   100     0.8153114  0.9225  0.42633341
##   2                   150     0.8182821  0.9040  0.47947837
##   2                   200     0.8214800  0.8910  0.51491415
##   2                   250     0.8209545  0.8780  0.53262769
##   2                   300     0.8209278  0.8655  0.54569007
##   2                   350     0.8203395  0.8595  0.55967398
##   2                   400     0.8193341  0.8560  0.56620735
##   2                   450     0.8187081  0.8520  0.57274071
##   2                   500     0.8177495  0.8475  0.58300369
##   2                   550     0.8172341  0.8470  0.58206912
##   2                   600     0.8160518  0.8430  0.58579005
##   2                   650     0.8150557  0.8335  0.58580309
##   2                   700     0.8142389  0.8285  0.58765486
##   2                   750     0.8129551  0.8265  0.59045860
##   2                   800     0.8114235  0.8235  0.58859378
##   2                   850     0.8106544  0.8230  0.58951967
##   2                   900     0.8098655  0.8225  0.58952402
##   2                   950     0.8089927  0.8195  0.59231471
##   2                  1000     0.8085903  0.8185  0.59044990
##   3                    50     0.8124471  0.9675  0.23434471
##   3                   100     0.8166505  0.9160  0.43008042
##   3                   150     0.8183159  0.8875  0.50374701
##   3                   200     0.8170682  0.8700  0.52424690
##   3                   250     0.8167332  0.8610  0.54665942
##   3                   300     0.8170788  0.8535  0.55690067
##   3                   350     0.8155400  0.8470  0.57181917
##   3                   400     0.8140688  0.8410  0.57181482
##   3                   450     0.8124477  0.8355  0.57367529
##   3                   500     0.8114718  0.8325  0.57367963
##   3                   550     0.8100906  0.8275  0.57740926
##   3                   600     0.8092354  0.8230  0.58113888
##   3                   650     0.8082420  0.8220  0.58859813
##   3                   700     0.8065477  0.8190  0.58766355
##   3                   750     0.8062263  0.8160  0.58858944
##   3                   800     0.8044913  0.8130  0.58765486
##   3                   850     0.8029262  0.8125  0.58765486
##   3                   900     0.8020108  0.8110  0.58858944
##   3                   950     0.8016405  0.8105  0.59045860
##   3                  1000     0.8011373  0.8090  0.59232775
##   4                    50     0.8139509  0.9640  0.24734188
##   4                   100     0.8150242  0.9120  0.43657900
##   4                   150     0.8179537  0.8850  0.49533145
##   4                   200     0.8176002  0.8710  0.53356227
##   4                   250     0.8162216  0.8615  0.55220170
##   4                   300     0.8159643  0.8490  0.56901543
##   4                   350     0.8141087  0.8445  0.57553141
##   4                   400     0.8131285  0.8430  0.57832645
##   4                   450     0.8114524  0.8385  0.58020430
##   4                   500     0.8104583  0.8335  0.58671158
##   4                   550     0.8089872  0.8265  0.58764182
##   4                   600     0.8078067  0.8240  0.59137144
##   4                   650     0.8064856  0.8230  0.59418387
##   4                   700     0.8051274  0.8200  0.59044121
##   4                   750     0.8038530  0.8205  0.59324495
##   4                   800     0.8030680  0.8205  0.59699196
##   4                   850     0.8023061  0.8190  0.59793088
##   4                   900     0.8011695  0.8185  0.59606607
##   4                   950     0.8000060  0.8160  0.59326668
##   4                  1000     0.7988982  0.8140  0.59045860
##   5                    50     0.8124004  0.9640  0.23430124
##   5                   100     0.8128960  0.9085  0.43658770
##   5                   150     0.8164498  0.8875  0.50560313
##   5                   200     0.8159795  0.8755  0.53263638
##   5                   250     0.8154252  0.8595  0.55782221
##   5                   300     0.8146149  0.8500  0.56622473
##   5                   350     0.8132774  0.8420  0.57460987
##   5                   400     0.8123588  0.8405  0.58207781
##   5                   450     0.8111443  0.8355  0.58207781
##   5                   500     0.8090119  0.8295  0.58767225
##   5                   550     0.8078390  0.8255  0.58488589
##   5                   600     0.8068005  0.8255  0.58954575
##   5                   650     0.8047019  0.8230  0.59045425
##   5                   700     0.8033723  0.8215  0.59231906
##   5                   750     0.8024794  0.8210  0.58951967
##   5                   800     0.8019000  0.8190  0.59232341
##   5                   850     0.8006418  0.8185  0.59512715
##   5                   900     0.7998935  0.8170  0.59605303
##   5                   950     0.7984835  0.8170  0.59698326
##   5                  1000     0.7970453  0.8165  0.59418822
## 
## Tuning parameter 'shrinkage' was held constant at a value of 0.01
## 
## Tuning parameter 'n.minobsinnode' was held constant at a value of 10
## ROC was used to select the optimal model using the largest value.
## The final values used for the model were n.trees = 450,
##  interaction.depth = 1, shrinkage = 0.01 and n.minobsinnode = 10.

Gradient boost model performance is 0.8222721

Naive Bayes model

model_nb <- train(x = diab, y = outcome,
                   metric = "ROC",
                   method = "nb",
                   trControl = myControl
)

model_nb

## Naive Bayes 
## 
## 768 samples
##   8 predictor
##   2 classes: 'No', 'Yes' 
## 
## No pre-processing
## Resampling: Bootstrapped (5 reps) 
## Summary of sample sizes: 154, 153, 153, 154, 154 
## Resampling results across tuning parameters:
## 
##   usekernel  ROC        Sens    Spec     
##   FALSE      0.8029047  0.8280  0.5801608
##    TRUE      0.7895701  0.8145  0.5745447
## 
## Tuning parameter 'fL' was held constant at a value of 0
## Tuning
##  parameter 'adjust' was held constant at a value of 1
## ROC was used to select the optimal model using the largest value.
## The final values used for the model were fL = 0, usekernel = FALSE
##  and adjust = 1.

Naive Bayes model performance is 0.8029047

models <- c("glm", "glmnet", "rf", "gbm", "naive")
glm <- max(model_glm$results$ROC)
glmnet <- max(model_glmnet$results$ROC)
rf <- max(model_rf$results$ROC)
gbm <- max(model_gbm$results$ROC)
naive <- max(model_nb$results$ROC)
AUC <- c(glm, glmnet, rf, gbm, naive)
df <- data.frame(models, AUC)
df<- df[order(df[,2], decreasing=TRUE), ]
knitr::kable(df)

	models	AUC
3	rf	0.8247223
2	glmnet	0.8242214
4	gbm	0.8222721
1	glm	0.8136093
5	naive	0.8029047

Here, we found rf model performed the best, and also there are not big differences between the models.

Future thoughts

I used different machine learning algorithms to predict Diabetes. Models showed similar performances except the naives bayes which performed worst. As we saw, our simple glm model performance was very close to other more advanced algorithms.

We can help doctors to predict Diabetes with accuracy around 83% by using 8 simple medical parameters.

Given current speed in generation and collection of types data by including additional predictors we can build even better models.

Until next time!

Serdar

Serdar Korur

Data Scientist and PhD in Molecular Biology

Serdar is a Data Scientist and PhD in Cell Biology